Imagine you want to build a clock, but annoyingly enough, you find yourself stuck several centuries in the past, and you don’t really know how to start. The first thing you need is something that “ticks” in a reliably steady cadence. Enter the pendulum. Pendulums swing back and forth pretty steadily. Pendulums started being used as regulators for clocks in the early 1600s. In fact, Galileo designed one of the very first ones, but never built it (evidently he was too busy making some other kind of gadget he called a “telescope”).
It was Christian Huygens who actually built (and patented) the first pendulum clock. Well, OK, he didn’t actually build it himself; he designed it, then hired a fellow Dutchman named Salomon Coster to put the thing together. It worked pretty well, but Huygens was nothing if not a stickler for accuracy (he was a mathematician and astronomer as well as an inventor), and he found a problem. The longer the arc of the pendulum, the more inaccurate it became. In other words, the “isochronism” of the pendulum (isochronism is anything occurring at regular intervals) degraded with bigger back-and-forth swinging.
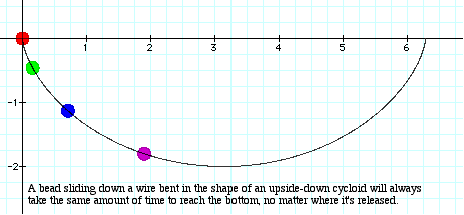
Huygens started looking into this, and a minor outcome of his research and experimentation was that he discovered a kind of curve that had a unique property. If you make, say, a wooden trough for a marble according to this curve, a marble dropped onto the trough at any point will take the same amount of time to reach the bottom. It’s a type of cycloid curve (a curve that repeats itself over and over in a cycle). If you imaging a spot on the side of a car’s tire, near the tread, then visualize the line that spot traces as the tire rotates along the road, that’s what the curve looks like. Kind of an upside-down arch, or a series of them placed end to end.
I mentioned that the cycloid curve (which Huygens used to make much more accurate pendulum clocks) was the minor outcome of his efforts. Sure, they use it in math and all that, but the biggest and most important result, obviously, was a new word: tautochrone. “Tautochrone” is what you call a curve with the property that an object placed anywhere on it takes the same amount of time to reach the bottom.
In fact there is only one tautochrone, and it’s the one Huygens discovered. “Chrone” comes from the Greek word for time, “chronos,” and “tauto” is also Greek — it means “the same.” Even though Huygens discovered the curve and invented the clock, though he didn’t coin the word (which is a shame; he probably would have become much more famous if he had). “Tautochrome” arose a bit later, and in France, not the Netherlands (where Huygens was from). Its first appearance in English was in Oliver Goldsmith’s Survey of Experimental Philosophy, considered in its Present State of Improvement in 1776.
The time around 1775 and 1776 seems to have been an exciting time for people who came up with new names for curves; they probably had their own club, although nobody thought to write any notes about it. “Brachistochrone” also showed up about then — that’s the curve that ensures an object placed on it at any point will reach the bottom in the shortest possible time. “Brachisto” comes from the Greek word for “brief.” There may have been some other sorts of world events going on in the world around that time, but come on — with “tautochrone” and “brachistochrone” being coined within a couple of years of each other, what else could have mattered?